Introduction
In many coding interviews, you may come across a question asking you to remove duplicate elements from a sorted array. This problem requires you to remove duplicate elements in place such that each unique element appears only once. The relative order of the elements should be kept the same. Then return the number of unique elements in nums.
Problem Statement
Given an integer array nums sorted in non-decreasing order, remove the duplicates in place such that each unique element appears only once. Then return the number of unique elements in nums.
Consider the number of unique elements of nums to be k, to get accepted, you need to do the following things:
Change the array nums such that the first k elements of nums contain the unique elements in the order they were present in nums initially.
The remaining elements of nums are not important as well as the size of nums.
Return k.
Algorithmic Approach
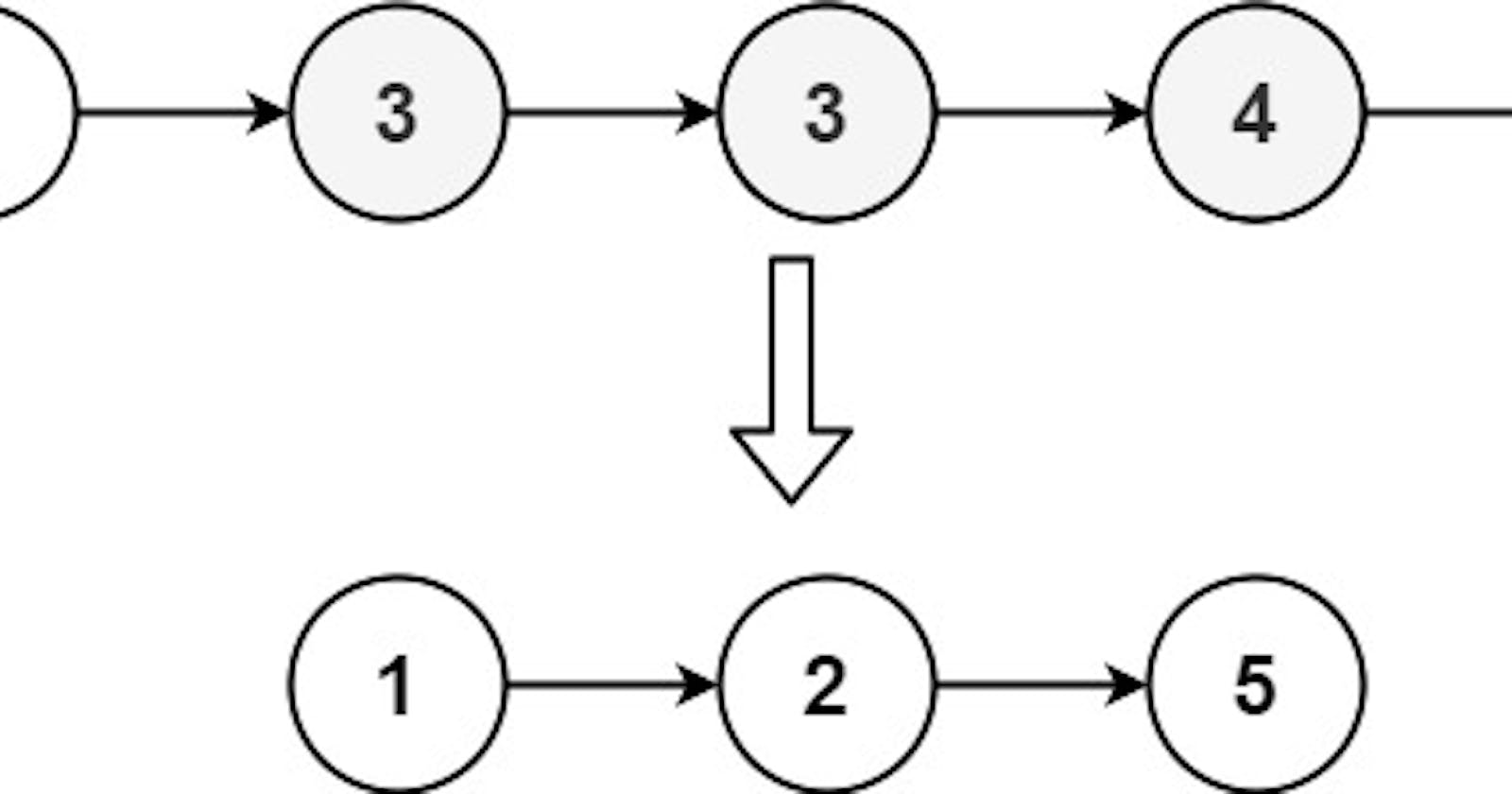
This code snippet uses a slightly different approach than the previous algorithm. It uses a vector V to store unique elements as they are encountered while iterating over the input array nums. The vector V is initialized empty, and for each element in nums, if the vector is empty or the last element of the vector is not equal to the current element of nums, we push the current element onto the vector. Once all unique elements have been identified and stored in V, we copy the contents of the vector back to the original nums array.
The algorithm then iterates over the vector V and copies its contents back to nums, starting at index 0. We keep track of the current index in nums using a variable i, which is incremented every time we copy an element from V to nums. We then return the value of i, which represents the number of unique elements in nums.
Code Implementation:
C++ Code:
int removeDuplicates(vector<int>& nums) {
vector<int> V;
for (int i = 0; i < nums.size(); i++) {
if (V.empty() || V.back() != nums[i]) {
V.push_back(nums[i]);
}
}
int i = 0;
while(!V.empty()){
nums[i++] = V.front();
V.erase(V.begin());
}
return i;
}
Python Code:
def removeDuplicates(self, nums: list[int]) -> int:
ans = 1
for i in range(1, len(nums)):
if nums[i] != nums[i - 1]:
nums[ans] = nums[i]
ans += 1
return ans
Time Complexity
The time complexity of this algorithm is O(n), where n is the length of the input array nums. This is because we iterate over the array once to identify and store unique elements in the vector V, and then iterate over the vector to copy its contents back to nums.
Space Complexity
The space complexity of this algorithm is O(n), where n is the length of the input array nums. This is because we store unique elements in the vector V, which can have a maximum size equal to the size of nums if all elements in nums are unique.
Conclusion
In this version of the algorithm, we saw how to use a vector to store unique elements as they are encountered while iterating over the input array. We then copied the contents of the vector back to the original nums array to remove duplicates. We also analyzed the time and space complexity of this algorithm. The algorithm approaches to achieve the same goal of removing duplicates from a sorted array and has linear time complexity, but the algorithm has a higher space complexity due to the use of a vector.